¿Qué es la Ecuación de Continuidad? Explicación y Aplicaciones en Física

Un vistazo a la Ecuación de Continuidad y su relevancia en la dinámica de fluidos

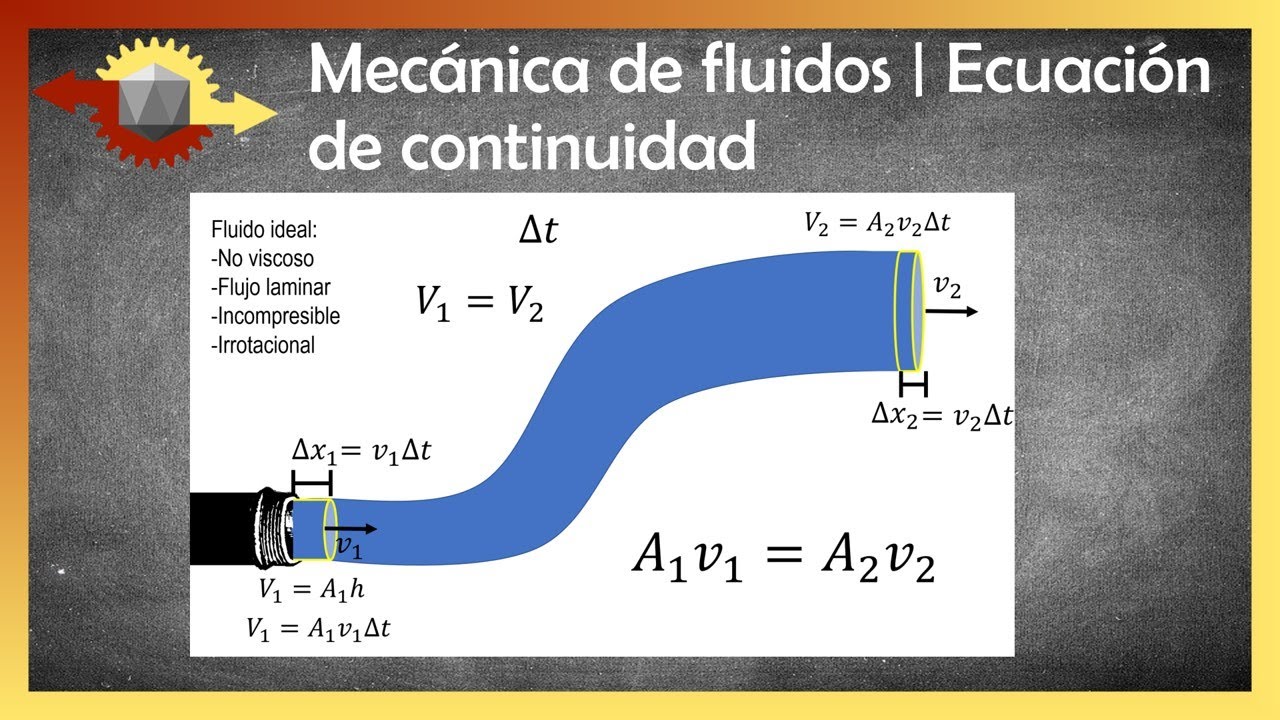
¿Alguna vez te has preguntado cómo el agua puede fluir a través de una manguera de jardín y, al mismo tiempo, salir disparada cuando aprietas la boquilla? Esta es la magia de la ecuación de continuidad. Esta relación fundamental en la física de fluidos nos ayuda a entender cómo se comportan los líquidos y gases al moverse a través de diferentes secciones de un conducto. Pero, ¿qué es exactamente la ecuación de continuidad? En términos simples, establece que, para un flujo incompresible (como el agua), el producto del área de la sección transversal de un conducto y la velocidad del fluido en esa sección es constante. Es decir, si el área disminuye, la velocidad tiene que aumentar, y viceversa. ¡Interesante, verdad? Ahora, vamos a desglosarlo más a fondo!

Fundamentos de la Ecuación de Continuidad

La ecuación de continuidad se puede expresar matemáticamente como:

A₁ * v₁ = A₂ * v₂

Donde:

• A₁ y A₂ son las áreas de las secciones transversales del conducto en dos puntos diferentes.
• v₁ y v₂ son las velocidades del fluido en esos puntos.

Ahora, hablemos de cómo se aplica esto en situaciones reales. Imagina que estás usando una manguera de jardín. Si abres el grifo lentamente, el agua sale de la manguera a una velocidad moderada. Pero si cubres parcialmente la boquilla con tu dedo, el área de salida se reduce. ¿Qué crees que pasa? Exactamente, el agua sale disparada a mayor velocidad. Esto es la ecuación de continuidad en acción. Es como si el fluido estuviera «presionado» a salir más rápido debido a la constricción del espacio.

Aplicaciones Prácticas de la Ecuación de Continuidad

Flujo en Tuberías

La ecuación de continuidad tiene aplicaciones cruciales en la ingeniería de fluidos. Por ejemplo, en el diseño de tuberías para el suministro de agua, es vital calcular las velocidades del agua en diferentes secciones para asegurar un flujo eficiente. Si el diseño no tiene en cuenta esta ecuación, podrías acabar con un sistema que no suministra suficiente agua a los hogares, o peor aún, que cause daños por presión excesiva.

Aerodinámica

En el mundo de la aviación, la ecuación de continuidad también juega un papel fundamental. Cuando un avión vuela, el aire fluye sobre y debajo de sus alas. La forma de las alas está diseñada de tal manera que el aire se mueve más rápido sobre la parte superior que debajo. Esto crea una diferencia de presión que produce sustentación. Sin la ecuación de continuidad, no podríamos entender cómo estos principios físicos permiten que los aviones vuelen.

Medición de Caudales

Otra aplicación importante es en la medición de caudales. Si quieres saber cuánto fluido pasa por un punto en particular en un tubo, puedes usar la ecuación de continuidad. Conocer el área de la sección transversal y la velocidad del fluido te permitirá calcular el caudal, lo cual es esencial en procesos industriales, sistemas de riego y más.

¿Qué pasa con los Fluidos Compresibles?

Es importante mencionar que la ecuación de continuidad también se aplica a fluidos compresibles, como los gases. Sin embargo, en este caso, la ecuación se complica un poco. A medida que un gas se mueve a través de un conducto, su densidad puede cambiar, lo que significa que la ecuación debe incluir un término de densidad. A pesar de esta complicación, el principio básico sigue siendo el mismo: el flujo se ajusta a la geometría del sistema.

El Impacto de la Ecuación de Continuidad en la Ciencia y la Tecnología

La ecuación de continuidad no solo es una herramienta matemática; es una piedra angular en muchas ramas de la ciencia y la tecnología. Desde la climatología, donde se estudian los flujos de aire en la atmósfera, hasta la ingeniería médica, donde se analizan flujos sanguíneos en el cuerpo humano, esta ecuación tiene aplicaciones prácticas que salvan vidas y mejoran la calidad de vida.

Simulaciones Computacionales

Hoy en día, con el avance de la tecnología computacional, la ecuación de continuidad se utiliza en simulaciones de dinámica de fluidos. Esto permite a los ingenieros y científicos modelar cómo se comportarán los fluidos en diferentes condiciones antes de construir sistemas reales. Es como tener una bola de cristal que te muestra cómo se comportará el agua en una nueva tubería o cómo el aire fluirá alrededor de un nuevo diseño de ala de avión.

Retos y Consideraciones

A pesar de su utilidad, la ecuación de continuidad tiene sus limitaciones. Por ejemplo, no considera factores como la viscosidad del fluido o las turbulencias, que pueden afectar el flujo real. En aplicaciones más complejas, como el flujo de sangre en el sistema circulatorio o el aire en un motor, se requieren ecuaciones más sofisticadas, como las ecuaciones de Navier-Stokes, que incluyen efectos de viscosidad y otros factores. Pero no te preocupes, eso no significa que la ecuación de continuidad no sea útil; simplemente se trata de saber cuándo y cómo utilizarla correctamente.

Conclusión

En resumen, la ecuación de continuidad es una de esas joyas de la física que, aunque puede parecer simple, tiene profundas implicaciones en el mundo real. Desde el agua que fluye por nuestras mangueras hasta los aviones que surcan los cielos, esta ecuación nos ayuda a comprender y predecir el comportamiento de los fluidos en una variedad de situaciones. Así que la próxima vez que veas agua fluyendo, recuerda que hay una historia matemática detrás de cada gota.

Preguntas Frecuentes

¿La ecuación de continuidad se aplica solo a líquidos?

No, aunque comúnmente se asocia con líquidos, también se aplica a gases, pero con consideraciones adicionales sobre la densidad.

¿Qué sucede si el fluido es viscoso?

En el caso de fluidos viscosos, se deben considerar otros factores como la fricción interna, lo que puede complicar la aplicación de la ecuación de continuidad.

¿Por qué es importante en la ingeniería?

Es crucial porque ayuda a diseñar sistemas eficientes que minimizan pérdidas de energía y garantizan un flujo adecuado en tuberías, canales y otros conductos.

¿Cómo se relaciona con el principio de Bernoulli?

La ecuación de continuidad es fundamental para entender el principio de Bernoulli, que relaciona la presión, la velocidad y la altura en el flujo de fluidos.

¿Existen limitaciones en su uso?

Sí, las limitaciones incluyen no considerar efectos como turbulencias o cambios en la temperatura y presión, especialmente en fluidos compresibles.