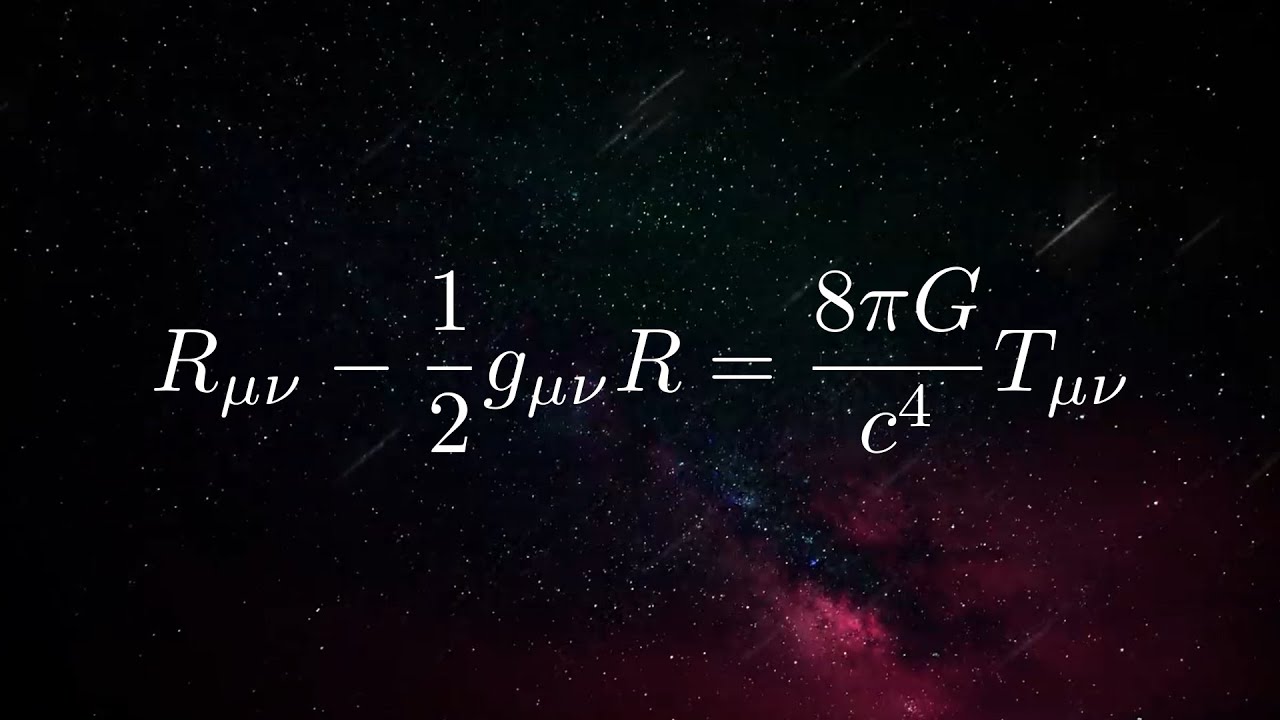Ecuaciones de Campo de Einstein: Todo lo que Necesitas Saber sobre la Relatividad General

Introducción a la Relatividad General y sus Implicaciones

La Relatividad General, propuesta por Albert Einstein en 1915, es una de las teorías más fascinantes y complejas que se han desarrollado en el campo de la física. Pero, ¿qué son exactamente las Ecuaciones de Campo de Einstein y por qué son tan importantes? Imagina que el universo es como una enorme tela de araña. Cada estrella, planeta y galaxia representa un punto en esa tela, y la gravedad actúa como un hilo que conecta todos esos puntos. Las Ecuaciones de Campo de Einstein son la forma matemática de describir cómo la materia y la energía influyen en la curvatura de esa tela, lo que a su vez afecta el movimiento de los objetos en el espacio. En este artículo, vamos a desglosar estos conceptos y explorar por qué son tan fundamentales para entender nuestro universo.

¿Qué son las Ecuaciones de Campo de Einstein?

Las Ecuaciones de Campo de Einstein son un conjunto de diez ecuaciones que forman la base de la Relatividad General. Estas ecuaciones describen cómo la geometría del espacio-tiempo se ve afectada por la presencia de masa y energía. En términos más simples, nos dicen cómo la gravedad no es solo una fuerza que actúa a distancia, sino una manifestación de la curvatura del espacio-tiempo. La famosa ecuación puede parecer intimidante al principio, pero no te preocupes; no necesitas ser un físico para entender sus implicaciones. Lo esencial es que estas ecuaciones nos permiten predecir fenómenos como la órbita de los planetas, el comportamiento de las ondas gravitacionales y la formación de agujeros negros.

El Contexto Histórico de la Relatividad General

Para entender la importancia de las Ecuaciones de Campo de Einstein, es útil retroceder un poco en la historia. Antes de Einstein, la visión clásica de la gravedad era la de Isaac Newton, quien la describió como una fuerza que actúa a distancia. Sin embargo, a medida que los científicos comenzaron a observar el universo a través de telescopios más potentes, se dieron cuenta de que había fenómenos que no podían explicarse con la teoría newtoniana. Por ejemplo, la órbita de Mercurio mostraba un comportamiento inusual que no encajaba con las predicciones de Newton. Fue entonces cuando Einstein llegó al escenario con su revolucionaria idea de que la gravedad es el resultado de la curvatura del espacio-tiempo.

Los Principios Fundamentales de la Relatividad General

Ahora bien, ¿cuáles son los principios que sustentan esta teoría? Primero, Einstein propuso que las leyes de la física son las mismas para todos los observadores, sin importar su estado de movimiento. Esto se conoce como el principio de equivalencia. En segundo lugar, introdujo la idea de que la masa de un objeto no solo afecta su movimiento, sino que también afecta la geometría del espacio-tiempo. En otras palabras, la presencia de masa «deforma» el espacio a su alrededor, creando lo que podríamos imaginar como una especie de «hoyo» en la tela de araña que mencionamos antes.

¿Cómo se Derivan las Ecuaciones de Campo de Einstein?

Las Ecuaciones de Campo de Einstein se derivan utilizando conceptos avanzados de geometría y cálculo tensorial, pero no es necesario ser un experto para entender la idea básica. Einstein utilizó el concepto de tensores, que son objetos matemáticos que permiten describir propiedades físicas en diferentes sistemas de referencia. En esencia, estas ecuaciones son una relación entre la geometría del espacio-tiempo (representada por el tensor métrico) y la distribución de la materia y energía en ese espacio (representada por el tensor de energía-momento).

La Forma Matemática de las Ecuaciones

Si bien no vamos a profundizar en las complejidades matemáticas, es importante mencionar que la forma más comúnmente citada de las Ecuaciones de Campo de Einstein es:

Gμν = 8πGTμν

Donde Gμν es el tensor de Einstein, que describe la curvatura del espacio-tiempo, Tμν es el tensor de energía-momento, que describe la distribución de la materia y energía, y G es la constante de gravitación universal. Este equilibrio entre la curvatura y la materia es lo que permite que las ecuaciones de Einstein describan una amplia variedad de fenómenos en el universo.

Las Implicaciones de las Ecuaciones de Campo de Einstein

Ahora que tenemos una comprensión básica de las Ecuaciones de Campo de Einstein, es hora de explorar algunas de sus implicaciones más sorprendentes. ¿Sabías que estas ecuaciones predicen la existencia de agujeros negros? Así es. Cuando la densidad de masa se concentra en un punto extremadamente pequeño, la curvatura del espacio-tiempo se vuelve tan intensa que nada, ni siquiera la luz, puede escapar de su atracción. Este es el fenómeno que conocemos como agujero negro, un concepto que ha fascinado a científicos y al público en general por igual.

Las Ondas Gravitacionales: Una Predicción que se Volvió Realidad

Otra de las predicciones más emocionantes de las Ecuaciones de Campo de Einstein son las ondas gravitacionales. Estas son perturbaciones en el espacio-tiempo que se producen cuando objetos masivos, como agujeros negros o estrellas de neutrones, colisionan. La existencia de estas ondas fue confirmada por primera vez en 2015 por el experimento LIGO, lo que marcó un hito en la historia de la física. La capacidad de detectar ondas gravitacionales no solo valida la Relatividad General, sino que también abre nuevas puertas para la observación del universo.

La Relatividad General y la Cosmología

Las Ecuaciones de Campo de Einstein no solo se aplican a objetos individuales, sino que también son fundamentales para la cosmología, el estudio del universo en su conjunto. Gracias a estas ecuaciones, los científicos pueden modelar la expansión del universo y entender fenómenos como la materia oscura y la energía oscura. La famosa ecuación de Friedmann, que describe la expansión del universo, se deriva directamente de las Ecuaciones de Campo de Einstein.

El Universo en Expansión

Una de las ideas más asombrosas que surgieron de la Relatividad General es que el universo no es estático; está en constante expansión. Esto fue una revelación sorprendente que cambió la forma en que entendemos el cosmos. La observación de que las galaxias se alejan unas de otras sugiere que el universo ha estado expandiéndose desde el Big Bang. Las Ecuaciones de Campo de Einstein permiten a los cosmólogos calcular cómo se comporta esta expansión y predecir su futuro.

¿Qué Sucede con la Relatividad General en Situaciones Extremas?

Las Ecuaciones de Campo de Einstein son increíblemente robustas, pero también plantean preguntas intrigantes en situaciones extremas. Por ejemplo, ¿qué ocurre en el centro de un agujero negro? Allí, las condiciones son tan extremas que la curvatura del espacio-tiempo se vuelve infinita, lo que lleva a lo que conocemos como «singularidades». En estas regiones, las leyes de la física tal como las conocemos dejan de ser aplicables, y los científicos aún luchan por comprender lo que realmente sucede.

La Búsqueda de una Teoría Unificada

Este misterio ha llevado a muchos físicos a buscar una teoría que unifique la Relatividad General con la mecánica cuántica, la teoría que describe el comportamiento de las partículas subatómicas. La gravedad, tal como se describe en la Relatividad General, y las fuerzas que rigen el mundo cuántico parecen ser incompatibles en ciertas situaciones. Esta búsqueda de una «teoría del todo» es uno de los mayores desafíos de la física moderna.

Preguntas Frecuentes

1. ¿Por qué las Ecuaciones de Campo de Einstein son tan importantes?
Las Ecuaciones de Campo de Einstein son fundamentales porque nos permiten entender cómo la gravedad funciona en el contexto de la relatividad, describiendo cómo la materia y la energía afectan la estructura del espacio-tiempo.

2. ¿Cómo se relacionan las Ecuaciones de Campo con los agujeros negros?
Las Ecuaciones de Campo predicen la existencia de agujeros negros al mostrar que la concentración extrema de masa puede crear una curvatura tan intensa en el espacio-tiempo que nada puede escapar de su atracción.

3. ¿Qué son las ondas gravitacionales y por qué son importantes?
Las ondas gravitacionales son perturbaciones en el espacio-tiempo producidas por eventos cósmicos masivos. Su detección ha proporcionado una nueva forma de observar el universo y ha validado la teoría de Einstein.

4. ¿La Relatividad General se aplica a la vida cotidiana?
Aunque la Relatividad General se centra en fenómenos a gran escala, como la gravitación en el espacio, sus efectos son también relevantes en situaciones cotidianas, como el funcionamiento del GPS, que debe tener en cuenta la dilatación del tiempo.

5. ¿Qué se está investigando actualmente en el campo de la relatividad?
Los científicos están investigando la relación entre la Relatividad General y la mecánica cuántica, buscando una teoría unificada que pueda explicar tanto los fenómenos a gran escala como los a nivel subatómico.