Ecuación de Continuidad en Física: Conceptos, Aplicaciones y Ejemplos Clave
Introducción a la Ecuación de Continuidad
La ecuación de continuidad es uno de esos conceptos que, aunque puede sonar complicado, en realidad tiene una lógica bastante sencilla. Imagina que tienes una manguera de jardín. Si aprietas la manguera en un punto, el agua sigue fluyendo, pero la velocidad del agua aumenta. Esto se debe a que el volumen de agua que pasa por un punto de la manguera en un tiempo determinado debe ser constante. ¡Y ahí es donde entra la ecuación de continuidad! Este principio se aplica no solo al agua, sino a cualquier fluido, ya sea aire, aceite o incluso gas en el espacio. A lo largo de este artículo, vamos a desglosar este concepto, ver cómo se aplica en diferentes situaciones y dar ejemplos que te ayudarán a entenderlo mejor.
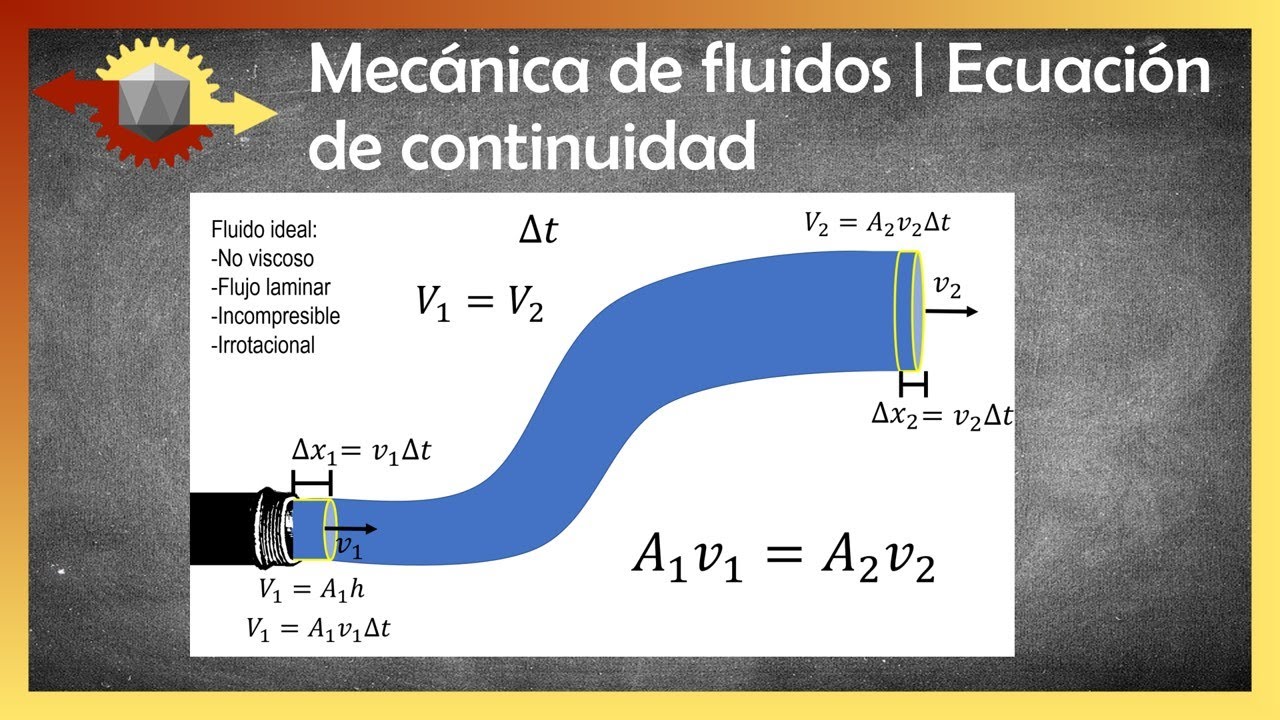
La ecuación de continuidad se expresa matemáticamente como A1V1 = A2V2, donde A es el área de la sección transversal del tubo y V es la velocidad del fluido. Pero antes de entrar en detalles sobre la fórmula, hablemos un poco más sobre lo que significa en términos prácticos. Cuando un fluido se mueve a través de un tubo, la cantidad de fluido que entra en un segmento del tubo en un tiempo determinado debe ser igual a la cantidad que sale. Si el área del tubo cambia (por ejemplo, se estrecha o se ensancha), la velocidad del fluido debe ajustarse para mantener esa continuidad. ¿Te imaginas si el agua se detuviera al apretar la manguera? ¡Sería un caos!
¿Qué es la Ecuación de Continuidad?
La ecuación de continuidad es una expresión de la conservación de la masa en un flujo de fluido. En términos simples, dice que, en un flujo estable, la masa de fluido que entra en un área determinada debe ser igual a la masa que sale. Esto se basa en la premisa de que la masa no se puede crear ni destruir, solo puede cambiar de forma o moverse de un lugar a otro.
Fundamentos de la Ecuación
Para entender mejor esta ecuación, pensemos en un tubo que tiene diferentes diámetros en diferentes secciones. Si el tubo es más estrecho en un punto, el fluido debe moverse más rápido para que la misma cantidad de fluido pueda pasar a través de él en el mismo tiempo. Por lo tanto, cuando el área del tubo disminuye (A2 < A1), la velocidad del fluido aumenta (V2 > V1). Por el contrario, si el área aumenta, la velocidad disminuirá. Este principio es fundamental en diversas aplicaciones, desde la ingeniería hasta la medicina.
Aplicaciones de la Ecuación de Continuidad
La ecuación de continuidad no es solo un concepto teórico; tiene aplicaciones prácticas en muchos campos. Vamos a ver algunas de ellas.
1. Ingeniería de Fluidos
En la ingeniería de fluidos, la ecuación de continuidad se utiliza para diseñar sistemas de tuberías y canales. Por ejemplo, al diseñar una red de tuberías para un sistema de agua potable, los ingenieros deben asegurarse de que el flujo de agua sea constante en todas las partes del sistema. Si una sección de la tubería es más estrecha, deben calcular cuánta presión se necesita para mantener el flujo adecuado.
2. Aerodinámica
En el ámbito de la aerodinámica, la ecuación de continuidad es crucial para entender cómo el aire se mueve alrededor de un avión. Cuando el aire se encuentra con el ala de un avión, se acelera al pasar por la parte superior del ala, donde el área es más pequeña. Esto es parte de lo que permite que el avión se eleve. Sin la ecuación de continuidad, no podríamos explicar adecuadamente cómo funcionan las alas.
3. Medicina
En medicina, la ecuación de continuidad se aplica en el flujo sanguíneo. Por ejemplo, al estudiar cómo la sangre fluye a través de las arterias y venas, los médicos pueden entender mejor ciertas condiciones médicas. Si una arteria se estrecha debido a una enfermedad, la velocidad de la sangre debe aumentar, lo que puede causar problemas.
Ejemplos Prácticos
Ahora que hemos cubierto los conceptos y aplicaciones, vamos a explorar algunos ejemplos prácticos que ilustran la ecuación de continuidad.
Ejemplo 1: Fluir en un Grifo
Imagina que abres el grifo de la cocina. Al principio, el agua fluye lentamente. Pero si cubres parcialmente la salida del grifo con tu mano, notarás que el agua sale con más fuerza. Esto es un ejemplo de la ecuación de continuidad en acción. Al reducir el área por donde sale el agua, la velocidad del agua aumenta.
Ejemplo 2: Ríos y Corrientes
Pensemos en un río. Cuando un río se estrecha, como al pasar por un cañón, el agua fluye más rápido. Si el río tiene una sección ancha y profunda, el flujo es más lento. Aquí también se puede ver la ecuación de continuidad en acción: el volumen de agua que pasa por un punto del río en un tiempo determinado se mantiene constante, independientemente de la forma del río.
Ejemplo 3: La Manguera de Jardín
Regresando a la manguera de jardín, si tienes una manguera que se ensancha a medida que avanza, el agua fluirá más despacio en la parte más ancha. Si apretas la manguera, la sección se vuelve más estrecha y el agua sale disparada. Esto muestra cómo la ecuación de continuidad se aplica en situaciones cotidianas.
¿Por Qué es Importante la Ecuación de Continuidad?
La ecuación de continuidad es fundamental porque nos ayuda a entender y predecir el comportamiento de los fluidos en diversas situaciones. Sin este principio, sería difícil diseñar sistemas eficientes, ya sea en ingeniería, medicina o incluso en nuestra vida diaria. Además, al comprender cómo los fluidos se comportan, podemos hacer ajustes en sistemas existentes para mejorar su rendimiento.
Impacto en el Medio Ambiente
Un aspecto interesante de la ecuación de continuidad es su relación con el medio ambiente. Al comprender cómo el agua fluye a través de ríos y arroyos, los ecologistas pueden diseñar mejores sistemas de conservación del agua y gestionar los recursos hídricos de manera más efectiva. Por ejemplo, al estudiar cómo el flujo de agua cambia en diferentes secciones de un río, pueden prever inundaciones y tomar medidas preventivas.
Preguntas Frecuentes
1. ¿La ecuación de continuidad se aplica solo a líquidos?
No, la ecuación de continuidad se aplica a cualquier tipo de fluido, ya sean líquidos o gases. Cualquier sustancia que fluya puede ser analizada utilizando este principio.
2. ¿Qué sucede si hay pérdida de masa en el sistema?
Si hay pérdida de masa, como en el caso de una fuga, la ecuación de continuidad ya no se aplicará en su forma más simple. En esos casos, se necesitarían ajustes en la ecuación para considerar la masa que se ha perdido.
3. ¿Se puede usar la ecuación de continuidad en situaciones no estacionarias?
Sí, aunque la ecuación de continuidad se basa en el principio de flujo estacionario, se pueden hacer adaptaciones para situaciones no estacionarias, considerando cómo cambia el flujo con el tiempo.
4. ¿La ecuación de continuidad se relaciona con la energía del fluido?
Sí, la ecuación de continuidad se relaciona con la ecuación de Bernoulli, que considera la energía en un flujo de fluido. Ambas ecuaciones son esenciales para entender el comportamiento de los fluidos.
5. ¿Por qué es importante entender la ecuación de continuidad en la vida diaria?
Entender la ecuación de continuidad puede ayudarte a tomar decisiones informadas sobre el uso del agua, el diseño de sistemas de riego, y la comprensión de cómo funcionan los sistemas de plomería en tu hogar.
En resumen, la ecuación de continuidad es un concepto fascinante y esencial en el mundo de la física y la ingeniería. No solo nos ayuda a comprender cómo se comportan los fluidos, sino que también tiene aplicaciones prácticas que impactan nuestras vidas diarias. Así que la próxima vez que uses una manguera o observes un río, piensa en cómo la continuidad del flujo está trabajando en segundo plano. ¡Es realmente impresionante!